Collection Update

Issue #119

This is about collection update, how to provide correct IndexPath and a simple diffing algorithm

• Excerpt from my talk at CocoaHeads, Oslo https://www.meetup.com/CocoaHeads-Oslo/events/244892347/
• Slide https://speakerdeck.com/onmyway133/collection-update

CollectionView

It’s hard to imagine of any apps that don’t use Table View or CollectionView. And by CollectionView, I actually mean UICollectionView 😉 . Most of the time, we show something with response from backend, then potentially update and insert new items as data changed.

We can totally call reloadData to reflect the changes, but an animation is better here as it gives user better understanding of what’s going on, and to not surprise them.

This talks about UICollectionView, but UITableView behaves the same

Drag and Drop

Let’s imagine an app where user are allowed to customise their experience by moving items from one collection to another.

You can take a look at the example DragAndDrop which is using the new drag and drop API in iOS 11.

You must ensure that your data is changed before calling update methods on UICollectionView. And then we call deleteItems and insertItems to reflect data changes. UICollectionView performs a nice animation for you

func collectionView(_ collectionView: UICollectionView, performDropWith coordinator: UICollectionViewDropCoordinator) {

  let destinationIndexPath = coordinator.destinationIndexPath
  let sourceIndexPath = coordinator.items.last?.dragItem.localObject as! IndexPath

  // remove
  sourceItems.remove(at: sourceIndexPath.item)
  sourceCollectionView.deleteItems(at: [sourceIndexPath])

  // insert
  destinationItems.insert(draggedItem, at: destinationIndexPath.item)
  destinationCollectionView.insertItems(at: [destinationIndexPath])
}

NSInternalInconsistencyException

If you have large number of items with many insertions and deletions from backend response, you need to calculate the correct IndexPath to call, which are not easy thing. Most the time you will get the following crashes

Terminating app due to uncaught exception ‘NSInternalInconsistencyException’,
reason: ‘Invalid update: invalid number of items in section 0.
The number of items contained in an existing section after the update (213)
must be equal to the number of items contained in that section before
the update (154), plus or minus the number of items inserted or
deleted from that section (40 inserted, 0 deleted) and plus
or minus the number of items moved into or out of
that section (0 moved in, 0 moved out).’

In my experience it happened randomly because everyone has different data. Although the message is very descriptive, it may take a while to figure it out.

Game of IndexPath

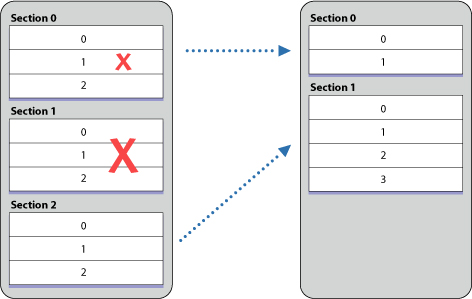
Let’s refine our knowledge of IndexPath by going through some examples. With a collection of 6 items, we perform some update operations and figure out what IndexPath should be.

items = ["a", "b", "c", "d", "e", "f"]

Take a look at my example here CollectionUpdateExample, there are many more examples

index vs offset

Before we go any further, I just want to mention that, by index I actually mean offset from the start. If you take a look at the enumerated function, it suggests the name as offset instead of index

Array(0..<10).enumerated().forEach { (offset, element) in

}

This zero based numbering could shed some light on this matter

Particularly in C, where arrays are closely tied to pointer arithmetic, this makes for a simpler implementation: the subscript refers to an offset from the starting position of an array, so the first element has an offset of zero.

1. Insert 3 items at the end

items.append(contentsOf: ["g", "h", "i"])

// a, b, c, d, e, f, g, h, i

let indexPaths = Array(6...8).map { IndexPath(item: $0, section: 0) }
collectionView.insertItems(at: indexPaths)

2. Delete 3 items at the end

items.removeLast()
items.removeLast()
items.removeLast()

// a, b, c

let indexPaths = Array(3...5).map { IndexPath(item: $0, section: 0) }
collectionView.deleteItems(at: indexPaths)

3. Update item at index 2

items[2] = "👻"

// a, b, 👻, d, e, f

let indexPath = IndexPath(item: 2, section: 0)
collectionView.reloadItems(at: [indexPath])

4. Move item “c” to the end

items.remove(at: 2)
items.append("c")

// a, b, d, e, f, c

collectionView.moveItem(
  at: IndexPath(item: 2, section: 0),
  to: IndexPath(item: 5, section :0)
)

5. Delete 3 items at the beginning, then insert 3 items at the end

With multiple different operations, we should use performBatchUpdates

You can use this method in cases where you want to make multiple changes to the collection view in one single animated operation, as opposed to in several separate animations. You might use this method to insert, delete, reload, or move cells or use it to change the layout parameters associated with one or more cells

items.removeFirst()
items.removeFirst()
items.removeFirst()

items.append(contentsOf: ["g", "h", "i"])

// d, e, f, g, h, i

collectionView.performBatchUpdates({
  let deleteIndexPaths = Array(0...2).map { IndexPath(item: $0, section: 0) }
  collectionView.deleteItems(at: deleteIndexPaths)

  let insertIndexPaths = Array(3...5).map { IndexPath(item: $0, section: 0) }
  collectionView.insertItems(at: insertIndexPaths)
}, completion: nil)

6. Insert 3 items at the end, then delete 3 items beginning

items.append(contentsOf: ["g", "h", "i"])

items.removeFirst()
items.removeFirst()
items.removeFirst()

// d, e, f, g, h, i

collectionView.performBatchUpdates({
  let insertIndexPaths = Array(6...8).map { IndexPath(item: $0, section: 0) }
  collectionView.insertItems(at: insertIndexPaths)

  let deleteIndexPaths = Array(0...2).map { IndexPath(item: $0, section: 0) }
  collectionView.deleteItems(at: deleteIndexPaths)
}, completion: nil)

🙀

If you run the example 6, you will get a crash

Terminating app due to uncaught exception 
'NSInternalInconsistencyException', 
reason: 'attempt to insert item 6 into section 0, 
but there are only 6 items in section 0 after the update'

performBatchUpdates

It is because the way performBatchUpdates works. If you take a look at the documentation

Deletes are processed before inserts in batch operations. This means the indexes for the deletions are processed relative to the indexes of the collection view’s state before the batch operation, and the indexes for the insertions are processed relative to the indexes of the state after all the deletions in the batch operation.

No matter how we call insert or delete, performBatchUpdates always performs deletions first. So we need to call deleteItems and insertItems as if the deletions occur first.

items.append(contentsOf: ["g", "h", "i"])

items.removeFirst()
items.removeFirst()
items.removeFirst()

// d, e, f, g, h, i

collectionView.performBatchUpdates({
  let deleteIndexPaths = Array(0...2).map { IndexPath(item: $0, section: 0) }
  collectionView.deleteItems(at: deleteIndexPaths)

  let insertIndexPaths = Array(3...5).map { IndexPath(item: $0, section: 0) }
  collectionView.insertItems(at: insertIndexPaths)
}, completion: nil)

Operations

There are many operations on UICollectionView, and there are operations to update whole section as well. Take a look Ordering of Operations and Index Paths

insertItems(at indexPaths: [IndexPath])
deleteItems(at indexPaths: [IndexPath])
reloadItems(at indexPaths: [IndexPath])
moveItem(at indexPath: IndexPath, to newIndexPath: IndexPath)
performBatchUpdates(_ updates, completion)

insertSections(_ sections: IndexSet)
deleteSections(_ sections: IndexSet)
reloadSections(_ sections: IndexSet)
moveSection(_ section: Int, toSection newSection: Int)

Edit distance

Doing these calculations by hand is quite tedious and error prone. We can build our own abstraction using some algorithms. The naive one is Wagner–Fischer algorithm which uses Dynamic Programming to tell the edit distance between two strings of characters.

Edit distance means the number of steps needed to change from one string to another. String is just a collection of characters, so we can generalise this concept to make it work for any collection of items. Instead of comparing character, we require items to conform to Equatable

“kit” -> “kat”

How can we transform form the word “kit” to “kat”? What kinds of operations do we nede to perform? You may tell “just change the i to a”, but this trivial example helps you understand the algorithm. Let’s get started.

Deletions

If we go from “kit” to an empty string “”, we need 3 deletions

“k” -> “” 👉 1 deletion
“ki” -> “” 👉 2 deletions
“kit” -> “” 👉 3 deletions

Insertions

If we go from an empty string “” to “kat”, we need 3 insertions

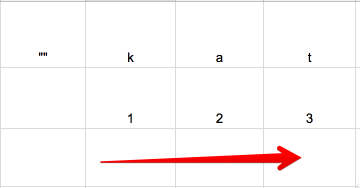
“” -> “k” 👉 1 insertion
“” -> “ka” 👉 2 insertions
“” -> “kat” 👉 3 insertions

If equal, take value from the top left

You can think of the algorithm as if we go from source string, to empty string, to destination string. We try to find the minimum steps to update. Going horizontally means insertions, vertically means deletions and diagonally means substitutions

This way we can build our matrix, iterate from row to row, column by column. First, the letter “k” from source collection is the same with letter “k” from destination collection, we simply take value from the top left, which is 0 substituion

If not equal

We continue with the next letter from the destination collection. Here “k” and “a” are not the same. We take minimum value from left, top, top left. Then increase by one

Here we take value from left, which is horizontally, so we increase by 1 insertion

“k” -> “kat” 👉 2 insertions

Continue, they are not the same, so we take value from left horizontally. Here you can see it kind makes sense, as to go from “k” to “kat”, we need 2 insertions, which is to insert letters “a” and “t”

The bottom right value

Continue with the next row, and next row until we got to the bottom right value, which gives you the edit distance. Here 1 substitution means that we need to perform 1 substitution to go from “kit” to “kat”, which is update “i” with “a’

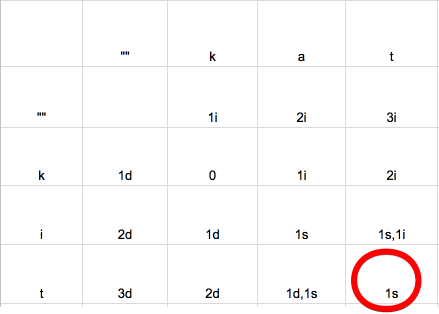
You can easily see that we need to update index 1. But how do we know that it is index 1 🤔

Edit steps

In each step, we need to associate the index of item in source and destination collection. You can take a look at my implementation DeepDiff

Complexity

We iterate through the matrix, with m and n are the length of source and destination collection respectively, we can see that the complexity of this algorithm is 0(mn).

Also the performance greatly depends on the size of the collection and how complex the item is. The more complex and how deep you want to perform Equatable can greatly affect your performance.

Improving performance

The section How does it work shows several ways we can improve performance.

Firstly, instead of building a matrix, which costs memory m*n, we can just use temporary arrays as holder.

Secondly, to quickly compare 2 items, we can use Hashable, as 2 identical items will always have the same hash.

More performance

If you want better performance, then algorithms with linear complexity may be interested to you. Take a look at Diff algorithm

• Heckel
• Wu
• Myers